Rotación
De Wikipedia, la enciclopedia libre

Rotación de la Tierra.
Rotación es el movimiento de cambio de orientación de un sólido extenso de forma que, dado un punto cualquiera del mismo, este permanece a una distancia constante del eje de rotación.
Una rotación pura de un cuerpo queda representada mediante el vector velocidad angular, que es un vector de carácter deslizante,  situado sobre el eje de rotación.
situado sobre el eje de rotación.
 situado sobre el eje de rotación.
situado sobre el eje de rotación.Rotación en sólidos rígidos
La velocidad angular de rotación está relacionada con el momento angular. Para producir una variación en el momento angular es necesario actuar sobre el sistema con fuerzas que ejerzan un momento de fuerza. La relación entre el momento de las fuerzas que actúan sobre el sólido y la aceleración angular se conoce como momento de inercia (I) y representa la inercia o resistencia del sólido a alterar su movimiento de rotación.
Para analizar el comportamiento cinemático de un sólido rígido debemos partir de la idea de que un ángulo θ define la posición instantánea de cualquier partícula contenida en el sólido rígido (CR); este ángulo se mide desde un plano perpendicular al eje de rotación del CR.
Si la posición queda completamente definida por la coordenada angular θ, entonces la velocidad del CR se podrá expresar como:
Mientras que la aceleración quedaría definida por:
La energía cinética de rotación se escribe:
siendo  la matriz de inercia.
la matriz de inercia.
 la matriz de inercia.
la matriz de inercia.La expresión del teorema del trabajo en movimientos de rotación se puede expresar así:
de modo que, la variación de la energía cinética del sólido rígido es igual al producto escalar del momento de las fuerzas por el vector representativo del ángulo girado (Δθ).
[editar] Transformaciones de rotación
En matemáticas las rotaciones son transformaciones lineales que conservan las normas en espacios vectoriales en los que se ha definido una operación de producto interior. La matriz de transformación tiene la propiedad de ser una matriz unitaria, es decir, es ortogonal y su determinante es 1.
Sea un vector A en el plano cartesiano definido por sus componentes x e y, descrito vectorialmente a través de sus componentes:
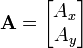
La operación de rotación del punto señalado por este vector alrededor de un eje de giro puede siempre escribirse como la acción de un operador lineal (representado por una matriz) actuando sobre el vector (multiplicando al vector:

En dos dimensiones la matriz de rotación para el vector dado puede escribirse de la manera siguiente:

Al hacer la aplicación del operador, es decir, al multiplicar la matriz por el vector, obtendremos un nuevo vector A' que ha sido rotado en un ángulo θ en sentido antihorario:

siendo
las componentes del nuevo vector después de la rotación.
[editar] Teorema de rotación de Euler
En matemáticas, el teorema de rotación de Euler dice que cualquier rotación o conjunto de rotaciones sucesivas puede expresarse siempre como una rotación alrededor de una única dirección o eje de rotación principal. De este modo, toda rotación (o conjunto de rotaciones sucesivas) en el espacio tridimensional puede ser especificada a través del eje de rotación equivalente definido vectorialmente por tres parámetros y un cuarto parámetro representativo del ángulo rotado. Generalmente se denominan a estos cuatro parámetros grados de libertad de rotación.
[editar] Composición de rotaciones en informática gráfica
En informática gráfica a veces existe cierta confusión sobre la interpretación de la composición de rotaciones en torno a los ejes (en el espacio euclídeo tridimensional), ya que la palabra 'ejes' puede referirse tanto a los ejes del sistema de referencia del mundo como a los ejes del sistema de referencia local.
Se explican desde 2 puntos de vistas: conceptual y teórico-mátemático en los 2 siguientes apartados.
[editar] Concepto de rotación y revolución
Puesto que a la rotación también se le llama, erróneamante, revolución, debemos diferenciar claramente el significado de estos términos.
- La rotación de un cuerpo alrededor de un eje (exterior o interior al cuerpo) corresponde a un movimiento en el que los distintos puntos del cuerpo presentan velocidades que son proporcionales a su distancia al eje. Obviamente, los puntos del cuerpo situados sobre el eje (en el caso de que este sea interior al eje) permanecen en reposo.
- La orientación del cuerpo en el espacio cambia continuamente durante la traslación.
- Un ejemplo de rotación el de la Tierra alrededor de su propio eje de rotación, con un periodo de rotación de un día sidéreo.
- La revolución de una partícula o de un cuerpo extenso corresponde a un movimiento de traslación del cuerpo sobre una trayectoria cerrada, no necesariamente circular.
- En este movimiento, la orientación del cuerpo en el espacio permanece constante.
- Un ejemplo de revolución es el de la Tierra alrededor de del Sol, con un periodo de revolución de un año.
La distinción entre rotación y revolución esta asociada con la existente entre rotación y traslación de un cuerpo extenso. El movimiento de traslación no prejuzga forma alguna para las trayectorias de los distintos puntos que constituyen el cuerpo. Evidentemente, si la velocidad de traslación es constante (v=cte), cada uno de los puntos del sólido recorrerá una trayectoria rectilínea con celeridad constante y todas esas trayectorias serán paralelas entre sí (movimiento de traslación uniforme). Pero, en general, la velocidad de traslación no tiene por que ser constante y la trayectoria puede ser curvilínea.
Las trayectorias recorridas por los distintos puntos del cuerpo pueden ser circunferencias, todas ellas del mismo radio (congruentes) aunque de distinto centro. Esta situación se presenta en una noria de feria de eje horizontal, como se muestra en la figura: la armadura de la noria gira en torno al eje (rotación), pero las barquillas suspendidas de dicha armadura, prescindiendo de pequeñas oscilaciones pendulares, experimentan una traslación con trayectorias circulares.
[editar] Rotación y revolución: punto de vista teórico-matemático
En informática gráfica a veces existe cierta confusión sobre la interpretación de la composición de rotaciones en torno a los ejes (en el espacio euclídeo tridimensional), ya que la palabra 'ejes' puede referirse tanto a los ejes del sistema de referencia del mundo como a los ejes del sistema de referencia local asociado a un objeto que sufre varias rotaciones (por tanto, estos ejes locales van cambiando con sucesivas rotaciones). Estas dos interpretaciones llevan a matrices de rotación distintas, y por tanto, si no se concreta, la mera referencia a una "composición de rotaciones en torno a los ejes" puede resultar ambigua.
Además, la rotación en torno a los ejes locales es aparentemente más compleja de expresar como una matriz que la rotación en torno a los ejes del sistema de referencia del mundo (SRM). Por otro lado, las rotaciones en torno a los ejes globales pueden provocar lo que se conoce como "Gimbal Lock". Sin embargo, como se demuestra más abajo, la obtención de ambas matrices es igual de sencilla, por lo tanto, para evitar el Gimbal Lock, podemos usar fácilmente las rotaciones en torno a los ejes locales.
Por ejemplo, supongamos que deseo rotar un objeto un ángulo  en torno al eje
en torno al eje  , después, un ángulo
, después, un ángulo  en torno al eje
en torno al eje  , y, finalmente, un ángulo
, y, finalmente, un ángulo  en torno al eje
en torno al eje  .
.
 en torno al eje
en torno al eje  , después, un ángulo
, después, un ángulo  en torno al eje
en torno al eje  , y, finalmente, un ángulo
, y, finalmente, un ángulo  en torno al eje
en torno al eje  .
.Supongamos que en todos los casos hablamos de rotaciones en torno a los ejes fijos del sistema de coordenadas del mundo. En este caso, la matriz de rotación  se obtiene como composición de otras tres, una por cada rotación:
se obtiene como composición de otras tres, una por cada rotación:
 se obtiene como composición de otras tres, una por cada rotación:
se obtiene como composición de otras tres, una por cada rotación:![\mathbf{}
M_1 ~=~ R[\mathbf{x},\alpha] \cdot R[\mathbf{y},\beta] \cdot R[\mathbf{z},\gamma]](http://upload.wikimedia.org/math/a/3/e/a3e2206afc5e1dc175671990d5500c1a.png)
donde la expresión
![\mathbf{}
R[\mathbf{u},a]](http://upload.wikimedia.org/math/b/b/c/bbc64c795ecb206c59ecdb270ae62d11.png)
hace referencia a la matriz de rotación de  radianes en torno a un vector
radianes en torno a un vector  arbitrario. Nótese que la expresión
arbitrario. Nótese que la expresión  expresa la matriz resultado de la composición de las matrices
expresa la matriz resultado de la composición de las matrices  y
y  , donde el efecto de aplicar
, donde el efecto de aplicar  a un vector
a un vector  es igual al efecto de aplicar primero
es igual al efecto de aplicar primero  y después
y después  a dicho vector, es decir, por definición:
a dicho vector, es decir, por definición:
 radianes en torno a un vector
radianes en torno a un vector  arbitrario. Nótese que la expresión
arbitrario. Nótese que la expresión  expresa la matriz resultado de la composición de las matrices
expresa la matriz resultado de la composición de las matrices  y
y  , donde el efecto de aplicar
, donde el efecto de aplicar  a un vector
a un vector  es igual al efecto de aplicar primero
es igual al efecto de aplicar primero  y después
y después  a dicho vector, es decir, por definición:
a dicho vector, es decir, por definición:
Supongamos ahora que intepretamos las rotaciones como rotaciones en torno a los ejes locales. La correspondiente matriz  es ahora:
es ahora:
 es ahora:
es ahora:![M_2 ~=~ R[\mathbf{x},\alpha] \cdot R[\mathbf{y}',\beta] \cdot R[\mathbf{z}'',\gamma]
\,\!](http://upload.wikimedia.org/math/2/d/8/2d836844394b423eab63b3044e689b1a.png)
donde
![\begin{matrix}
\mathbf{y'} & = & R[\mathbf{x},\alpha]\,\mathbf{y} \\
\mathbf{z'} & = & R[\mathbf{x},\alpha]\,\mathbf{z} \\
\mathbf{z''} & = & R[\mathbf{y},\beta]\,\mathbf{z'} \\
\end{matrix}](http://upload.wikimedia.org/math/d/9/3/d9380031f52e9a00007a992cbd1804a8.png)
Por tanto,  evita el Gimbal Lock pero es más compleja de obtener, puesto que está expresada en términos de rotaciones en torno a vectores que no coinciden con los ejes. Sin embargo, en realidad esto no es así, puesto que se puede demostrar que:
evita el Gimbal Lock pero es más compleja de obtener, puesto que está expresada en términos de rotaciones en torno a vectores que no coinciden con los ejes. Sin embargo, en realidad esto no es así, puesto que se puede demostrar que:
 evita el Gimbal Lock pero es más compleja de obtener, puesto que está expresada en términos de rotaciones en torno a vectores que no coinciden con los ejes. Sin embargo, en realidad esto no es así, puesto que se puede demostrar que:
evita el Gimbal Lock pero es más compleja de obtener, puesto que está expresada en términos de rotaciones en torno a vectores que no coinciden con los ejes. Sin embargo, en realidad esto no es así, puesto que se puede demostrar que:![M_2 ~=~ R[\mathbf{z},\gamma]\cdot R[\mathbf{y},\beta] \cdot R[\mathbf{x},\alpha]
\,\!](http://upload.wikimedia.org/math/5/2/5/52521be4013f474a93eb1900e2114a35.png)
es decir,  puede escribirse como composición respecto de los ejes del sistema de referencia del mundo, solo que en este caso la composición debe hacerse en el orden contrario respecto al orden que queremos para las rotaciones en torno a los ejes locales.
puede escribirse como composición respecto de los ejes del sistema de referencia del mundo, solo que en este caso la composición debe hacerse en el orden contrario respecto al orden que queremos para las rotaciones en torno a los ejes locales.
 puede escribirse como composición respecto de los ejes del sistema de referencia del mundo, solo que en este caso la composición debe hacerse en el orden contrario respecto al orden que queremos para las rotaciones en torno a los ejes locales.
puede escribirse como composición respecto de los ejes del sistema de referencia del mundo, solo que en este caso la composición debe hacerse en el orden contrario respecto al orden que queremos para las rotaciones en torno a los ejes locales.Para demostrar esta igualdad basta con aplicar dos propiedades de las matrices de rotación. La primera es que una rotación de un cierto ángulo obviamente se cancela si se compone con otra rotación igual pero con el ángulo cambiado de signo, es decir:
![R[\mathbf{u},a]\cdot R[\mathbf{u},-a]~~=~~I
\,\!](http://upload.wikimedia.org/math/d/5/0/d50bc152a298ac24008b1449fcf4eaf2.png)
donde  es la matriz identidad. La otra propiedad que se usará es esta:
es la matriz identidad. La otra propiedad que se usará es esta:
 es la matriz identidad. La otra propiedad que se usará es esta:
es la matriz identidad. La otra propiedad que se usará es esta:![R[R[\mathbf{u},a]\mathbf{v},b] ~~=~~ R[\mathbf{u},-a]\cdot R[\mathbf{v},b]\cdot R[\mathbf{u},a]
\,\!](http://upload.wikimedia.org/math/1/0/5/105ebb3007d3ff93f3186c3cc0cd2396.png)
que se cumple para cualesquiera vectores  y
y  y ángulos
y ángulos  y
y 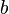 . Significa que, para rotar en torno al vector
. Significa que, para rotar en torno al vector ![\mathbf{v}'=R[\mathbf{u},a]\,\!](http://upload.wikimedia.org/math/a/6/9/a698cdd38b657407818f9f2237a9019e.png) (que es
(que es  rotado en torno a
rotado en torno a  ), podemos: (1) deshacer la rotación en torno a
), podemos: (1) deshacer la rotación en torno a  , (2) hacer la rotación en torno al vector original
, (2) hacer la rotación en torno al vector original  , y (3) rehacer de nuevo la rotación en torno a
, y (3) rehacer de nuevo la rotación en torno a  .
.
 y
y  y ángulos
y ángulos  y
y 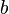 . Significa que, para rotar en torno al vector
. Significa que, para rotar en torno al vector ![\mathbf{v}'=R[\mathbf{u},a]\,\!](http://upload.wikimedia.org/math/a/6/9/a698cdd38b657407818f9f2237a9019e.png) (que es
(que es  rotado en torno a
rotado en torno a  ), podemos: (1) deshacer la rotación en torno a
), podemos: (1) deshacer la rotación en torno a  , (2) hacer la rotación en torno al vector original
, (2) hacer la rotación en torno al vector original  , y (3) rehacer de nuevo la rotación en torno a
, y (3) rehacer de nuevo la rotación en torno a  .
.Aplicando esta última propiedad varias veces en el orden adecuado (y cancelando las rotaciones complementarias que aparecen) podemos demostrar fácilmente que la segunda expresión de  se deriva de la definición original.
se deriva de la definición original.
e adjunta una imagen para demostración de artificios 3D, partiendo de una imagen 2D, que no tiene nada que ver con la rotación, aunque el efecto final parezca ser así, pues el resultado consiste en pegar partes definidas a un área restringida una detrás de otra. Es una ilusión óptica que nuestro cerebro interpreta como una rotación de acuerdo a los datos que sobre el objeto (la cabeza) retiene nuestra memoria. se deriva de la definición original.
se deriva de la definición original.




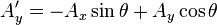


No hay comentarios:
Publicar un comentario